Ao se findar o século XVI, um dos grandes desafios da matemática consistia em encontrar meios de simplificar os cálculos aritméticos, de escoimá-los de erros, visando em especial às necessidades da astronomia. Alguns procedimentos então usados com essa finalidade estavam longe do ideal. Era o caso da prostaférese (adição e subtração em grego), consistindo na conversão de produtos em somas, mediante relações trigonométricas como por exemplo:
Esse ponto de estrangulamento seria eliminado com a criação dos logaritmos no século XVII. É interessante notar que, embora os logaritmos resultem da relação inversa da potenciação, à época em que surgiram ainda não se usavam expoentes em matemática. Sem dúvida são dois os pais da idéia de logaritmo:John Napier (1550 – 1617) e Jobst Bürgi (1552 – 1632), em trabalhos independentes, quase concomitantes,o primeiro a partir de noções geométricas, o segundo a partir de noções algébricas. E há também os precursores, dos quais talvez o mais importante seja Michael Stifel (1487 – 1567).
Alemão da cidade de Esslinger, Stifel seguiu a carreira religiosa, inicialmente como monge agostiniano, mas acabou se convertendo às doutrinas de Lutero, de quem era amigo. Às tantas, certamente sem consultar seu líder religioso, anunciou o fim do mundo para 3/10/1533, baseando-se em interpretações de profecias bíblicas. Considerando-se sua grande reputação científica e a intensidade da fé naquela época, pode-se imaginar os transtornos causados por esse rebate falso. Tanto que Stifel teve que se refugiar numa prisão... De lá Lutero o salvou para a matemática.
Com efeito, em 1544 Stifel publicaria sua Arithmetica integra, o mais importante tratado de álgebra da Alemanha no século XVI. Nele aparece pela primeira vez o triângulo dos coeficientes do binômio, até os de ordem 17, inclusive a fórmula recorrente entre eles hoje conhecida como relação de Stifel. E aparece também o embrião da idéia de logaritmo. Cotejando a progressão geométrica:
com a progressão aritmética:
Stifel observou que o produto (quociente) de dois termos quaisquer da primeira está associado à soma (diferença) dos respectivos da segunda. Mas para que a idéia fosse proveitosa, era preciso interpolar, numa e na outra, cópias associadas convenientes de números reais, algo muito difícil para a época.
O suíço Bürgi era um homem eclético. Dedicava-se à fabricação de relógios, mas era versado em matemática e astronomia, tendo mesmo colaborado com Kepler em Praga. Daí, provavelmente, sua preocupação em criar os logaritmos, embora fosse um exímio calculista.
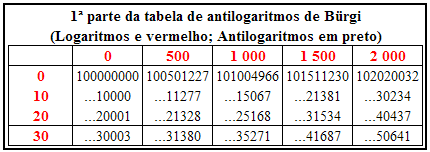
Estimulado pelas idéias de Stifel,partiu de uma progressão aritmética de primeiro termo igual a 0, razão igual a 10 e último termo igual a 32.000, cujos elementos chamou de números vermelhos (pela cor com que os imprimiu). A progressão geométrica correspondente começa com 108 e razão é 1 + 10– 4 (notação atual), seus termos são chamados números negros. A partir daí constrói o que na verdade é, na terminologia atual, uma tábua de antilogaritmos: os números vermelhos (logaritmos) são escritos na primeira linha e na coluna da esquerda e os negros correspondentes distribuídos pelas demais linhas e colunas. A escolha de 1,0001 como razão da P.G. objetivava fazer com que suas potências ficassem muito próximas entre si; e começar essa progressão com 108 era um expediente ara evitar números decimais.
Bürgi inventou seus logaritmos por volta do ano 1600. Mas somente em 1620 publicou um trabalho a respeito. Com isso ficou atrás de Napier na questão da prioridade sobre o assunto.
Texto de Hygino H. Domingues
Veja mais:
Os Logaritmo Segundo Napier
Utilizando Tábuas para Calcular Logaritmos
Utilizando Tábuas para Encontrar Aproximações de Raízes
Utilizando Tábuas para Encontrar Aproximações de Expressões Complexas




Postar um comentário