Construção Geométrica de PHI em Circunferências (Parte 3)

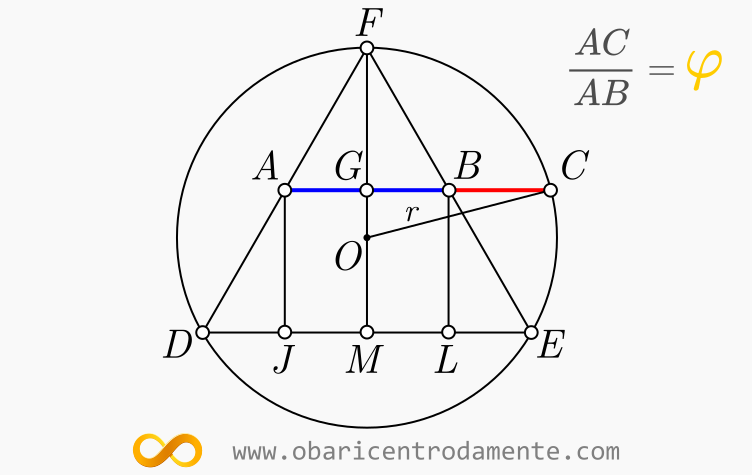
Esta construção foi desenvolvida por George Odom, publicada no American Mathematics Monthy, em 1983 e se dá com a circunferência circunscrita a um triângulo equilátero. Tomando os pontos médios de dois lados do triângulo, unimos esses pontos por um segmento de reta prolongando-o até a intersecção com a circunferência. A razão entre os segmentos $AC$ e $AB$ é PHI.

Sendo a os lados do triângulo equilátero inscrito à circunferência, temos que encontrar as medidas dos segmentos $AC$ e $AB$.

Considerando a figura abaixo, notem que, se $DF = a$, logo:

$$AF = \frac{a}{2} = AB \tag{1}$$

Vamos determinar primeiramente a medida da altura $MF$ do triângulo:

$$DF^2 = MF^2 + DM^2\\ \ \\ a^2 = MF^2 + \frac{a^2}{4}\\ \ \\ MF^2 = a^2-\frac{a^2}{4}\\ \ \\ MF^2 = \frac{2a^2}{3}$$

Extraindo a raiz de ambos os lados da igualdade, obtemos:

$$MF = \frac{a\sqrt{3}}{2} \tag{2}$$

Como $DE=DJ+JL+LE=a$ e $\displaystyle JL=AB=\frac{a}{2}$, logo, o segmento $DJ$ é igual a:

$$DJ = \frac{a}{4} \tag{3}$$

Vamos determinar a medida de $AJ$:

$$AD^2 = DJ^2 + AJ^2\\ \ \\ \frac{a^2}{4} = \frac{a^2}{16} + AJ^2\\ \ \\ AJ^2 = \frac{a^2}{4} - \frac{a^2}{16}\\ \ \\ AJ^2 = \frac{3a^2}{16}$$

Extraindo a raiz de ambos os lados da igualdade, obtemos:

$$AJ = \frac{a\sqrt{3}}{4} \tag{4}$$

Analisando a figura 2, vemos que:

$$\begin{cases} \displaystyle OM = \frac{1}{3} MF\\ \displaystyle AJ = OG + \frac{1}{3}MF \end{cases}$$

Da segunda equação, temos:

$$OG = AJ - \frac{1}{3}MF\\ \ \\ OG = \frac{a\sqrt{3}}{4} - \frac{a\sqrt{3}}{6}\\ $$

Obtendo:

$$OG = \frac{a\sqrt{3}}{12} \tag{5}$$

Podemos aplicar o teorema pitagórico no triângulo retângulo $OGC$, onde $r$ é o raio da circunferência que equivale a $2/3$ de sua altura:

$$r = \frac{2}{3}MF\\ \ \\ r = \frac{a\sqrt{3}}{3} \tag{6}$$

Temos que:

$$r^2 = OG^2 + GC^2\\ \ \\ \left(\frac{3a^2}{3}\right)^2 = \left(\frac{a\sqrt{3}}{12}\right)^2 + GC^2\\ \ \\ \frac{3a^2}{9} = \frac{3a^2}{144} + GC^2$$

O segmento $AC=AG+GC$, assim $\displaystyle AG=\frac{a}{4}$. Logo:

$$AC = \frac{1}{4} + \frac{a\sqrt{5}}{4}\\ \ \\ AC = \frac{a\big( 1 + \sqrt{5} \big)}{4} \tag{8}$$

A razão áurea nesta construção é dada por $\displaystyle \frac{AC}{AB} = \varphi$:

$$\varphi = \frac{\displaystyle \frac{a\big(1+\sqrt{5}\big)}{4}}{\displaystyle \frac{a}{2}}\\ \ \\ \varphi = \frac{a\big(1+\sqrt{5}\big)}{4}\cdot \frac{2}{a}\\ \ \\ \varphi = \frac{1+\sqrt{5}}{2}\\ \ \\ \varphi = 1,618\cdots$$

Notem que esta construção independe do raio da circunferência.

Veja mais:

• #1 Construção geométrica de PHI
  
• #2 Construção geométrica de PHI
  
• #3 Construção geométrica de PHI
  
• #4 Construção geométrica de PHI
  
• #5 Construção geométrica de PHI
  
• #6 Construção geométrica de PHI
  
• #7 Construção geométrica de PHI
  
• #8 Construção geométrica de PHI