Vimos em outra oportunidade como determinar uma fração geratriz de dízima periódica utilizando o método de múltiplos. Neste post, vamos aprender a utilizar o conceito da PG para determinarmos a fração geratriz.
Primeiramente, vamos relembrar que a fórmula para determinar a soma dos termos de uma PG infinita é dada por:
Vamos tomar alguns exemplos que foram utilizados no post sobre Fração Geratriz através de múltiplos, para efeito de comparação.
Exemplo 1: Determinar a fração geratriz da dízima periódica 0,121212...
Podemos reescrever a dízima em forma de soma de frações:
Temos que o primeiro termo da PG infinita é:
E a razão desta PG é dada por:
Aplicaremos estes valores na fórmula da soma dos termos dada em (1):
Exemplo 2: Determinar a fração geratriz da dízima periódica 1,484848...
Vamos reescrever a dízima em forma de soma de frações:
Separamos a parte inteira e trabalharemos somente com a parte fracionária. Temos que o primeiro termo da PG infinita é:
E a razão desta PG é:
Aplicaremos estes valores na fórmula da soma dos termos dada em (1):
Agora, somamos o resultado encontrado em (5) com a parte inteira:
Exemplo 3: Determinar a fração geratriz da dízima periódica 1,06818181...
Vamos reescrever a dízima em forma de soma de frações:
Notamos que neste exemplo, além da parte inteira, contém uma parte decimal não periódica.
Separamos a parte inteira e trabalharemos somente com a parte fracionária. Temos que o primeiro termo da PG infinita é:
E a razão desta PG é:
Agora, aplicamos estes valores na fórmula da soma dos termos da PG infinita:
Somamos o resultado encontrado em (7) com a parte inteira da dízima e com a parte não periódica:
Veja Mais:
Fração Geratriz de Dízimas Periódicas
Fórmula da Soma dos Termos de uma P.G. Finita
Fórmula da Soma dos Termos de uma P.G. Infinita
Raízes em Progressões no Blog Fatos Matemáticos

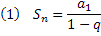

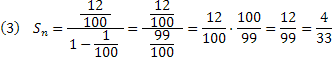
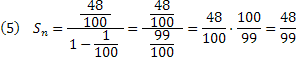
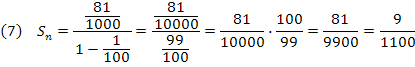

Muito bom o post parceiro. Fica a dica de fazer um post sobre PG, provando as fórmulas de soma finita e infinita. Obrigado pelo link citado. Abraços!
ResponderExcluirOlá parceiro. Dica aceita. Na verdade, estava com esse material à mão. Logo preparo um post.
ResponderExcluirForte abraço!
Ok.Legal
ResponderExcluirOlá,acho que teve um pequeno erro no terceiro exemplo,quando foi colocado 4 noves ao invés de 2.Mas de qualquer formao seu bog é foda.Abraços !
ResponderExcluirOlá amigo. Tem razão. Já foi corrigido. Obrigado por relatar o erro.
ExcluirUm abraço!
Muito bom, o seu blog!
ResponderExcluirE se eu tivesse por exemplo o número 33,323232....?
ResponderExcluirEscrevemos 33,323232... como:
Excluir$$32 + \frac{32}{100}+\frac{32}{10000}+{32}{1000000}+\ldots$$
Separamos a parte inteira da fracionária, sendo o primeiro termo da PG:
$$a_1 = \frac{32}{100}$$
cuja razão é:
$$q = \frac{1}{100}$$
Aplicando na fórmula da soma dos termos de uma PG:
$$S_n = \frac{a_1}{1-q}$$
obtemos:
$$S_n = \frac{\cfrac{32}{100}}{1-\cfrac{1}{100}} = \frac{\cfrac{32}{100}}{\cfrac{99}{100}} = \frac{32}{100}\cdot\frac{100}{99}=\frac{32}{99}$$
Somando à parte inteira:
$$33 + \frac{32}{99} = \frac{3299}{99}$$
E se tivesse, por exemplo, o número 0,05777...?
ResponderExcluirJoão, antes de qualquer coisa, sugiro que veja esse outro artigo: Frações Geratrizes
ExcluirAgora veja a resolução:
Podemos escrever $0,0577...$ como:
$$
x=0,0577\cdots
$$
Como existem 2 algarismos entre a vírgula e a parte periódica, multiplicamos ambos os lados por $100$:
$$
100x=5,777\cdots
$$
Assim:
$$
100x = 5 + 0,777\cdots
$$
Chamemos $y=0,777\cdots$. Então:
$$
100x = 5+y
$$
Agora, vamos achar a fração que gere $0,777\cdots$:
$$
y=0,777\cdots\\
10y=7,777\cdots\\
10y=7+0,777\cdots\\
10y=7+y\\
9y=7\\
y=\frac{7}{9}
$$
Retomando:$100x = 5+y$:
$$
100x = 5+\frac{7}{9}\\
100x = 52/9\\
x=\frac{52}{900}\\
x=0,05777\cdots
$$