O simples fato geométrico de que a tangente a uma curva é uma boa aproximação da curva próximo ao ponto de tangência $P$, pode ser usado para obter valores aproximados de funções.
Vamos estimar o valor de uma função $f(x)$ quando $x$ é um número próximo de um número conhecido.

Vamos estimar o valor de uma função $f(x)$ quando $x$ é um número próximo de um número conhecido.

[Figura 1]
Seja $f$ uma função continua num intervalo $I=\left [ a,b \right ]$. Suponha que $x_1$ é um número pertencente ao intervalo $I$ e ao domínio de $f$ e que $y_1=f(x_1)$ seja conhecido.
Sendo $f$ diferenciável em $x_1$, então a reta tangente à curva em $P=f(x_1,y_1)$ tem um coeficiente angular dado por $m=f^\prime=(x_1)$. O coeficiente angular de uma reta é definido por:
\displaystyle{m=\frac{y-y_1}{x-x_1}}
\end{equation}
Analisando a figura 1, podemos escrever a equação $(1)$ como:
\displaystyle{m=\frac{f(x_1+\Delta x)-f(x_1)}{(x_1+\Delta x)-x_1}=\frac{\Delta x}{\Delta y}}
\end{equation}
Se $\Delta x \rightarrow 0$, então $Q\rightarrow P$ e
\begin{equation}\displaystyle{m=\lim _{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}}
\end{equation}
Que é a definição de derivada, logo:
\begin{equation}m=f^\prime (x_1)
\end{equation}
Substituindo $(4)$ em $(1)$, obtemos:
$$\displaystyle{f^\prime(x_1)=\frac{y-y_1}{x-x_1}}$$
$$y-y_1=f^\prime (x_1)(x-x_1)$$
\begin{equation}
y=y_1+f ^\prime (x_1)(x-x_1)
\end{equation}
Fazendo $x=x_1+\Delta x$, notem que quando $x$ se aproxima de $x_1$ a altura do gráfico de $f$ acima de $(x,0)$ é aproximadamente igual à altura da reta tangente nesse ponto. Ou seja, $f(x)$ é aproximadamente o mesmo que:
$$y_1+f^\prime (x_1)(x-x_1)$$
Este é um processo de aproximação linear, já que é baseado no uso da reta tangente.
Sendo $f$ diferenciável em $x_1$ e que $y_1=f(x_1)$ é conhecido, então para valores de $x$ próximos de $x_1$, temos que:
$$f(x) \approx y_1+f^\prime (x_1)(x-x_1)$$
que é o mesmo que:
\begin{equation}f(x)\approx f(x_1)+f^\prime (x_1)(x-x_1)
\end{equation}
Exemplo 1: Aproxime $1/1,03$ usando o processo de aproximação linear.
Seja $\displaystyle f(x)=\frac{1}{x}$. Sua derivada será: $\displaystyle f^\prime(x)=-\frac{1}{x^2}$. Sabemos que o valor para $1/1,03$ é próximo de $1$. Fazemos então $x_1=1$. Assim:
\begin{matrix}\frac{1}{1,03}&=&f(1,03)\approx f(1)+f^\prime (1)(1,03-1)\\&=&1+\frac{(-1)}{1^2}(1,03-1)=0,97\\
\end{matrix}
Pela calculadora, temos que a divisão dada com quatro casas decimais corretas é $0,9709$.
Exemplo 2: Aproxime $\sqrt{1,02}$ usando o procedimento de aproximação linear.
Neste caso, $f(x)=\sqrt{x}$ e sua derivada será: $\displaystyle f^\prime (x)=\frac{1}{2\sqrt{x}}$. Tomando $x_1=1$, que é um valor próximo de $\sqrt{1,02}$, temos:
\begin{matrix}\sqrt{1,02}&=&f(1,02) \approx f(1)+f^\prime (1)(1,02-1) \\ &=&1+\frac{1}{2}(0,02)=1,01 \\
\end{matrix}
O valor exato até a quinta casa decimal é $1,00995$.
Por mais que escolhamos uma valor $x_1$ próximo de $x$, sempre será uma aproximação (muitas vezes, muito boa), pois sempre haverá um erro. Por isso, esse processo de aproximação é limitado.
O erro $E$ do processo de aproximação linear é dado por:
$$E=V_v-V_a$$
onde $V_v$ é o valor verdadeiro e $V_a$ é o valor aproximado. Assim:
$$E=f(x)-\biggr[f(x_1)-f^\prime (x_1)(x-x_1)\biggr]$$
Vejam que o erro depende de $x$, determinando uma função $E$ dada pela equação:
\begin{equation}E(x)=f(x)-f(x_1)-f^\prime (x_1)(x-x_1)
\end{equation}
Geometricamente, $E(x)$ é a diferença entre a altura acima de $(x,0)$ do gráfico de $f$ e a altura acima de $(x,0)$ da reta tangente a esse gráfico em $(x_1,y_1)$.
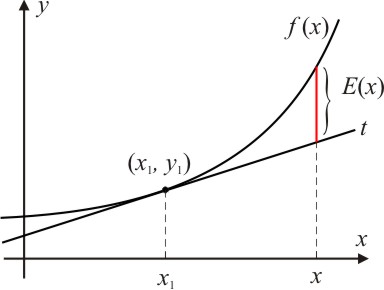
[Figura 2]
Notem que:
\begin{equation}\lim _{x \rightarrow x_1} E(x)=\lim _{x \rightarrow x_1} \biggr[f(x)-f(x_1)-f^\prime (x_1)(x-x_1) \biggr]=0
\end{equation}
De modo que o erro $E(x)$ tende a zero quando $x$ se aproxima de $x_1$. Na verdade, o fato mais importante é perceber que quando $x$ tende a $x_1$, $E(x)$ tende a zero tão rapidamente quanto a razão $\displaystyle \frac{E(x)}{x-x_1}$ continua tendendo a zero.
Quando $x$ tende a $x_1$, o denominador $x-x_1$ tende a zero, mas o numerador $E(x)$ tende a zero tão rapidamente que a influência do denominador é desprezada.
Para vermos que o limite $\displaystyle \lim_{x \rightarrow x_1} \frac{E(x)}{x-x_1}=0$, fazemos:
\begin{matrix}\lim_{x \rightarrow x_1} \frac{E(x)}{x-x_1}&=&\lim_{x \rightarrow x_1} \frac{f(x)-f(x_1)-f^\prime (x_1)(x-x_1)}{x-x_1}\\
&=& \lim_{x \rightarrow x_1}\biggr[\frac{f(x)-f(x_1)}{x-x_1}-f^\prime(x_1)\biggr]\\
&=& \lim_{x \rightarrow x_1}\biggr[\frac{f(x)-f(x_1)}{x-x_1} \biggr]-f^\prime(x_1)\\
\end{matrix}
Seja $\Delta x=x-x_1$. Assim $x=\Delta x+x_1$ e a condição $x \rightarrow x_1$ é equivalente à condição $\Delta x \rightarrow 0$. Segue que:
\begin{matrix}
\lim_{x \rightarrow x_1} \frac{E(x)}{x-x_1}&=&\lim_{\Delta x \rightarrow 0}\biggr[ \frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}\biggr] -f^\prime(x_1)\\
&=& f^\prime(x_1)-f^\prime(x_1)=0\\
\end{matrix}
Exemplo 3: Aproxime a raiz cúbica $\displaystyle \sqrt[3]{1,008}$ e calcule o erro da aproximação.
Fazemos $f(x)=\sqrt[3]{x}$ e sua derivada será $\displaystyle f^\prime (x)=\frac{1}{3x^{2/3}}$. Uma boa aproximação é 1, assim, $x_1=1$.
$$\sqrt[3]{1,008}\approx f(1)+f^\prime \left(1\right)(1,008-1)$$
$$\sqrt[3]{1,008}\approx1,002666\cdots$$
O valor real para $\sqrt[3]{1,008}$ até a sexta casa decimal é $1,002659$. Vejam que o valor aproximado é muito bom.
O erro $E(x)$ da aproximação é dado por:
$$E(x)=(1,002659)-1-\frac{1}{3}(1,008-1)=-7,6\times 10^{-6}$$
Realmente um erro muito pequeno, mas ainda assim é apenas uma aproximação. Para aplicações no mundo real, talvez fosse aceitável uma aproximação com $50$ casas decimais.
Links para este artigo:
Referências:
- Cálculo - Munem-Foulis
- Cálculo com Geometria Analítica - Simmons
Veja mais:
- Aplicação de Derivadas Para Determinação de Máximos e Mínimos
- Utilizando Tábuas de Logaritmos Para Encontrar Aproximações de Raízes
- Algumas Observações Sobre Notação de Derivada



ótimo post, parabéns!
ResponderExcluirsó há um pequeno erro no exemplo 3 quando se coloca f' (1/3) ao invés de colocar f'(1) que é igual a 1/3.
Olá Danimax, obrigado pelo comentário e pelo aviso. Já havia colocado o resultado antes! Já está corrigido.
ResponderExcluirAbraços!
Bela exposição. As equações ficaram muito bem renderizadas no meu navegador. A série de Taylor para expansão de funções igualmente nos fornece certa aproximação para funções de uma, duas, três, etc variáveis, sendo agora necessário o uso da convergência. Parabéns.
ResponderExcluirMeu caro João Elias, aumentei a fonte de 16px para 17px e realmente as fórmulas ficaram mais nítidas.
ResponderExcluirAqui no blog tem um pequeno estudo sobre a série de Taylor baseado em notas de aula, veja:
http://obaricentrodamente.blogspot.com.br/2010/03/expansao-em-serie-de-taylor.html
Há vários métodos para aproximar funções, depende de nossa percepção saber em que situação usar um ou outro método.
Um abraço!
Olá,
ResponderExcluirA dedução da Fórmula de Taylor segue por esse caminho.
O seu texto termina com "...talvez fosse aceitável uma aproximação com 50 casas decimais."
Como você chegou neste número de 50 casas?
Abraços,
Antonio
Olá Antonio.
ExcluirTem uma história que os mísseis Patriot usados na guerra do golfo em 1990 começaram a não atingir os mísseis inimigos Scud. Gastaram-se milhões para o desenvolvimento dos mísseis e não estavam cumprindo com sua função básica, pelo contrário, permitia os mísseis inimigos acertarem o alvo e ainda os próprios Patriots acertavam alvos não programados.
Descobriram uma falha no arredondamento na vigésima quarta casa decimal de uma conta (em base 2). O que fizeram foi aumentar a precisão para 50 casas decimais.
No link abaixo tem uma pequeno texto sobre.
http://www.diale.org/patriot.html
Eu sei que não podemos generalizar para qualquer aplicação, e o número de 50 casas decimais, claro, vai depender de cada uma delas. O fato é que podemos lidar com aproximações sem qualquer problema. Para cálculos corriqueiros podemos usar $\pi=3,14$ apenas, ou ainda mesmo como 3. Depende.
Agradeço pelo comentário. Um abraço!