Por: Sebastião Vieira do Nascimento (Sebá)
Teorema de Sebá: Todo número P (par) > 4, múltiplo de 4, pode ser escrito como diferença de dois quadrados de inteiros, P = x2 – y2, de uma ou mais maneiras diferentes, por meio das duas equações:
Nas quais: k são os divisores de P, k ≠ 2n + 1, 2 ≤ k2 < P e 2k tem que dividir P.
Demonstração:
Como P = x2 – y2, logo:
Como x e y são inteiros positivos, logo, x – y são os divisores de P.
Se x – y = k, então:
Temos o seguinte sistema de equações:
Resolvendo-o, obtém-se:
Note que se k2 ≥ P, implica x – k ≤ 0, logo, 2 ≤ k2 < P.
Se k = 2n + 1, P + k2 será ímpar, consequentemente, 2k (par) não divide P + k2 (ímpar):
Exemplo 1: De quantas maneiras diferentes pode-se escrever 16 = x2 – y2?
O divisor de 16, tal que 2 ≤ k2 < 16, é: 2.
Para k = 2 e P = 16:
Caso escolhêssemos k = 4, teríamos k2 = 42 = 16 = P, e obter-se-ia:
Exemplo 2: De quantas maneiras diferentes pode-se escrever 32 = x2 – y2?
Os divisores de 32, tal que 2 ≤ k2 < 32, são : 2 e 4.
Logo, 32 pode ser escrito como diferença de dois quadrados de duas maneiras diferentes.
Para k = 2 e P = 32:
Para k = 4 e P = 32:
Caso escolhêssemos k = 8 (um dos divisores de 32) teríamos k2 = 82 = 64 > P, e obter-se-ia:
Pelo teorema extraído de um livro de teoria dos números:
Se n é par:
Para n = 32, k = 8, logo:
Conclusão: Pelo teorema extraído de um livro de teoria dos números, 32 só pode ser escrito de uma única maneira como diferença de dois quadrados; já pelo teorema de Sebá, 32 pode ser escrito de duas maneiras diferentes como diferença de dois quadrados:
Flagrante Da Vida Real
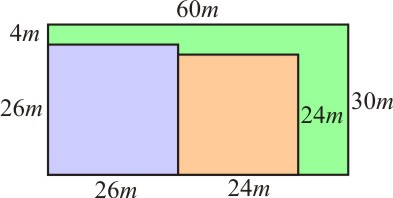
João, irmão de José, também possui um terreno retangular, cujas medidas são 30m x 60m e quer dividi-lo em lotes menores. Quer separar um lote de Ym2 para o cultivo de hortaliças e o restante quer dividi-lo em outros dois lotes quadrados para criar animais, de tal modo que a diferença entre esses dois lotes seja igual a 100m2. Pergunta-se:
a) Em quantas formas diferentes João pode dividir a parte de seu terreno destinada à criação de animais, obedecendo a suas exigências?
b) Quais as medidas de cada lote?
c) Quanto sobra de área do terreno para o cultivo de hortaliças para cada situação acima?
Resolução:
João quer dividir seu terreno, assim como seu irmão José, em lotes menores seguindo uma lei matemática um tanto incomum. Podemos imaginar que José e João são apreciadores da Matemática e, porque não, da teoria dos números.
Os divisores de 100, tal que 2 ≤ k2 < 100, são: 2 e 4.
Para k = 2 e P =100:
Para k = 4 e P = 100:
Vejam que esta solução não serve porque 14,52 e 10,52 não são dois quadrados de inteiros.
Resposta:
a) João pode separar o terreno em apenas uma forma.
b) As medidas dos lotes são:
Lote 1 possui 26m x 26m = 676m2
Lote 2 possui 24m x 24m = 576m2
c) O terreno de João possui medidas de 30m x 60m = 1.800m2. Sendo assim, ao dividi-lo em lotes conforme as formas encontradas em b), temos que as áreas que sobram para o cultivo de hortaliças será:
Vemos que existe apenas uma forma de dividir o terreno em lotes de modo a atender as exigências de João.
Este artigo foi cedido gentilmente por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB, além de colaborador deste blog. Foram feitas algumas alterações do manuscrito original para melhor exposição.
Veja mais:
Método Para Escrever Um Número Ímpar Composto Como Diferença De Dois Quadrados De Inteiros (Parte 1)
O Problema da Doação dos Terrenos e os Ternos Pitagóricos
Critérios de Divisibilidade por Qualquer Número Primo Maior que Onze

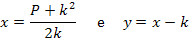

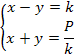

Postar um comentário