Por: Sebastião Vieira do Nascimento (Sebá)
O teorema abaixo foi extraído de um livro de teoria dos números.
Teorema 1: Um número inteiro n pode ser escrito como a diferença de dois quadrados de inteiros, n = x2 – y2, se e somente se n é ímpar ou múltiplo de 4.
Demonstração do mesmo livro:
Uma forma direta de obter a representação de n como diferença de dois quadrados é a seguinte:
Se n é múltiplo de 4:
Se n é ímpar:
Teorema de Sebá: Todo número ímpar (I), maior que a unidade, pode ser escrito como diferença de dois quadrados de inteiros: I = x2 – y2, de uma ou mais maneiras diferentes, por meio das duas equações:
Onde k são os divisores de I, tal que 1 ≤ k2 < I.
Demonstração:
Como I = x2 – y2, logo:
Como x e y são inteiros positivos, logo, x – y são os divisores de I.
Se x – y = k, então:
Temos o seguinte sistema de equações:
Resolvendo-o, obtém-se:
Note que se k2 ≥ I, implica x – k ≤ 0, logo, 1 ≤ k2 < I.
Exemplo 1: De quantas maneiras diferentes pode-se escrever 121 = x2 – y2?
Os divisores de 121, tal que 1 ≤ k2 < 121, é: 1. Logo, pode-se escrever 121 = x2 – y2 de uma única maneira.
Para k = 1 e I = 121:
Assim:
Caso escolhêssemos k = 11, teríamos k2 = 112 = 121= I, e obter-se-ia:
Exemplo 2: De quantas maneiras diferentes pode-se escrever o primo 13 = x2 – y2?
O divisor de 13, tal que 1 ≤ k2 < 13, é: 1. Logo, pode-se escrever 13 = x2 – y2 de um única maneira como diferença de dois quadrados.
Para k = 1 e I = 13:
Assim:
Exemplo 3: De quantas maneiras diferentes pode-se escrever 117 = x2 – y2?
Os divisores de 117, tal que 1 ≤ k2 < 117, são: 1, 3 e 9. Logo, temos três maneiras diferentes de escrever 117 como diferença de dois quadrados.
Modo 1: Para k = 1 e I = 117:
Assim:
Modo 2: Para k = 3 e I = 117:
Logo:
Modo 3: Para k = 9 e I = 117:
Assim:
Caso escolhêssemos k = 13, teríamos k2 = 132 = 169 > 117, e obter-se-ia:
Pelo teorema extraído de um livro de teoria dos números:
Se n é ímpar:
Se n = 117, k = 58, logo:
Conclusão: Pelo teorema extraído de um livro de teoria dos números, 117 só poderia ser escrito de uma única maneira como diferença de dois quadrados; já pelo Teorema de Sebá, o número 117 pode ser escrito de três maneiras diferentes como diferença de dois quadrados:
Flagrante Da Vida Real
José possui um terreno retangular cujas medidas são 60m x 110m e quer dividi-lo em lotes menores. Quer separar um lote de Xm2 para o cultivo de hortaliças e o restante quer dividi-lo em outros dois lotes quadrados para criar animais, de tal modo que a diferença entre esses dois lotes seja igual a 105m2. Pergunta-se:
a) Em quantas formas diferentes José pode dividir a parte de seu terreno destinada à criação de animais, obedecendo a suas exigências?
b) Quais as medidas de cada lote?
c) Quanto sobra de área do terreno para o cultivo de hortaliças para cada situação acima?
Resolução:
José quer dividir seu terreno em lotes menores seguindo uma lei matemática um tanto incomum. Podemos imaginar que José, no mínimo, é apreciador da Matemática.
Os divisores de 105, tal que 1 ≤ k2 < 105, são: 1, 3, 5 e 7.
De acordo com as fórmulas deduzidas acima, temos:
Para k = 1 e I = 105:
Assim:
Para k = 3 e I = 105:
Assim:
Para k = 5 e I = 105:
Assim:
Para k = 7 e I = 105:
Assim:
Resposta:
a) José pode separar o terreno em quatro formas distintas.
b) As medidas dos lotes são:
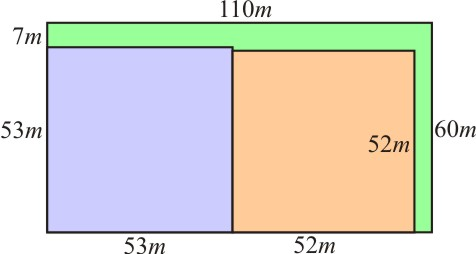
Forma 1:
Lote 1 possui 53m x 53m = 2.809m2
Lote 2 possui 52m x 52m = 2.704m2
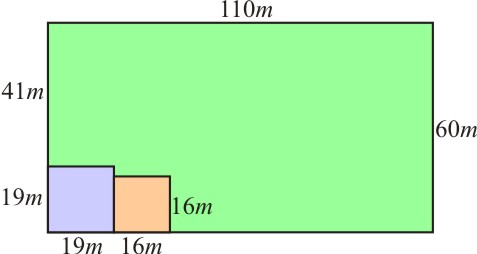
Forma 2:
Lote 1 possui 19m x 19m = 361m2
Lote 2 possui 16m x 16m = 256m2
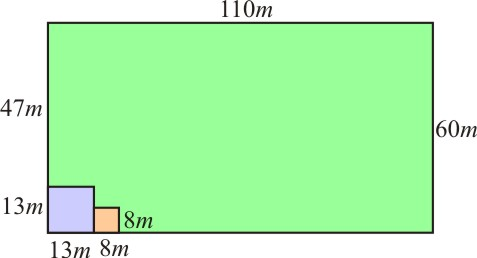
Forma 3:
Lote 1 possui 13m x 13m = 169m2
Lote 2 possui 8m x 8m = 64m2
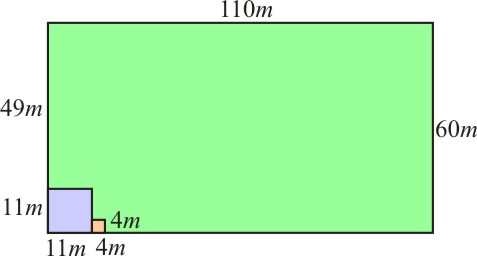
Forma 4:
Lote 1 possui 11m x 11m = 121m2
Lote 2 possui 4m x 4m = 16m2
c) O terreno de José possui medidas de 60m x 110m = 6.600m2. Sendo assim, ao dividi-lo em lotes conforme as formas encontradas em b), temos que as áreas que sobram para o cultivo de hortaliças será:
Para a forma 1:
Para a forma 2:
Para a forma 3:
Para a forma 4:
Vemos que existem 4 formas diferentes de dividir o terreno em lotes de modo a atender as exigências de José. Sendo assim, ele terá que decidir qual das quatro configurações é melhor para aplicar em sua realidade.
Este artigo foi cedido gentilmente por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB, além de colaborador deste blog. Foram feitas algumas alterações do manuscrito original para melhor exposição.
Veja mais:
Método Para Escrever um Número Par Como Diferença de Dois Quadrados (Parte 2)
Critérios de Divisibilidade por Qualquer Número Primo Maior que Onze
Método de Resolução das Equações de Sebá Parte 1, Parte 2, Parte 3

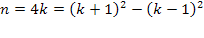

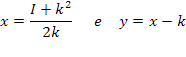

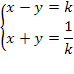
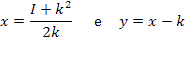
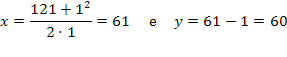
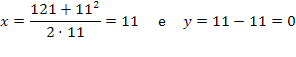
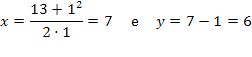
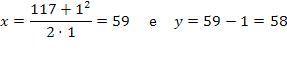

Muito obrigado!
ResponderExcluir