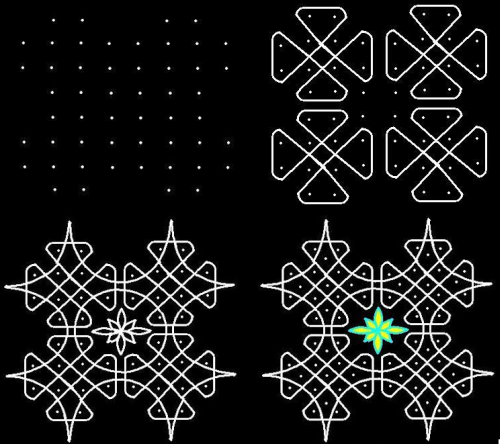
Num vilarejo no sudeste da Índia, em Tamil Nadu (Terra dos Tâmiles), todas as manhãs as mulheres saem de suas casas e iniciam um ritual: varrem a soleira da porta, espirram uma mistura de esterco de vaca e água, depois cobrem a área com figuras complexas elaboradas com pó-de-arroz. Segundo a tradição, o esterco de vaca limpa e purifica o solo, enquanto o pó-de-arroz constitui uma oferenda, pois é apreciado pelas formigas e é bom começar o dia com um ato de bondade.
As figuras desenhadas no solo são chamadas de Kolam e representa um sinal de graça e é prova de destreza, disciplina mental e capacidade de concentração. As figuras Kolam chamam a atenção em vários aspectos: é um exemplo incrível de expressão matemática num contexto cultural e vem cada vez mais chamando a atenção de profissionais em informática especializados na análise e descrição de imagens.
A tradição do Kolam perdura há séculos em Tamil Nadu, com uma literatura que remonta o século III a.C.. Passada de mãe para filha e é praticada por mulheres de todas as classes sociais, mas nos últimos anos, substituíram o arroz por pó-de-pedra, giz ou mesmo tinta.
Para fazer uma figura de Kolam, o ponto de partida é frequentemente uma tabela de pontos traçada no chão prevendo a forma e o tamanho do desenho, podendo ser uma rede retangular, triangular, ou mesmo hexagonal. A figura é então desenhada ligando os pontos ou contornando-os, de forma que os pontos guiem e determinem restrições do desenho.
Algumas figuras são constituídas por apenas uma linha contínua, que termina no ponto onde começou. Essas figuras são fechadas e associadas ao ciclo infinito do nascimento, fertilidade e morte e aos conceitos de continuidade, totalidade e eternidade. Outras figuras são constituídas por múltiplas curvas.
Há também famílias de figuras que podem partilhar características. Em vários casos figuras maiores combinam várias cópias justapostas de menores. Em outros casos, os membros são derivados um dos outros de forma sutil.
A concepção e organização das famílias são ricas em ideias matemáticas. Esses agrupamentos tem chamado a atenção dos teóricos da informática que trabalham com a análise e a descrição de imagens como o uso de linguagens gráficas. Essas linguagens trabalham basicamente com regras formais específicas para combinar essas unidades. Esse trabalho é aparentado com a teoria formal da linguagem, que foi descoberta há cerca de 50 anos com o estudo de Noam Chomsky sobre linguagens naturais.
Uma linguagem determinista fora de contexto foi utilizada para descrever uma outra família de figuras do Kolam, chamada Os Braceletes de Krishna, cujos membros são derivados recursivamente uns dos outros. Para desenhar Os Braceletes de Krishna, três movimentos ou operações são suficientes:
L → Avança descrevendo um traço;
D → Avança fazendo uma curva de 90° graus à direita;
A → Avança fazendo uma argola completa pela direita.
Segundo esses movimentos, cada um deles pode assumir as seguintes formas:
A figura inicia com uma cadeia de comandos que obedece a seguinte regra:
DLALALALD
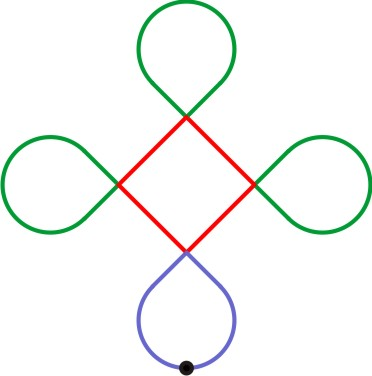
Esta é uma figura iterativa, ou seja, para cada etapa k, obtemos uma nova figura mais elaborada que partilha das mesmas características da figura original. Traduzindo para a linguagem gráfica, obtemos:
Etapa k = 0:
Para cada etapa k > 0, devemos aplicar uma regra de reescrita, definida por:
L → L
D → DLALD
A → DLALALALD
O que fazemos na etapa k é reescrever a sequência k – 1 substituindo cada movimento seguindo as regras de reescrita. Assim, para a etapa seguinte, temos:
Etapa k = 1:
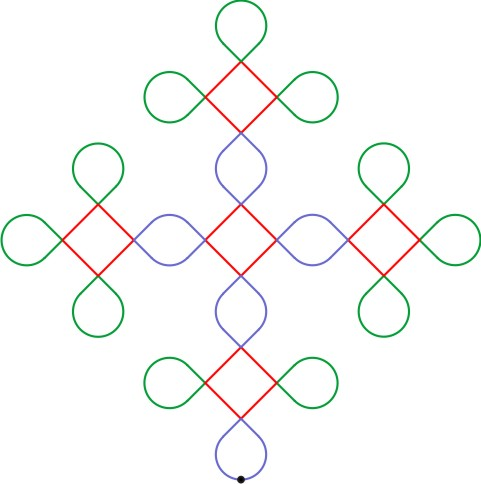
Substituímos as regras de reescrita na curva original, obtendo:
DLALD L
DLALALALD L DLALALALD L DLALALALD
L DLALD
Traduzindo para a linguagem gráfica, obtemos a figura:
Etapa k = 2:
Substituímos as regras de reescrita na curva de iteração k = 1:
DLALD L
DLALALALD L DLALD L DLALD L DLALALALD L DLALALALD L DLALALALD L DLALD L DLALD L DLALALALD L DLALALALD L DLALALALD L DLALD L DLALD L DLALALALD L DLALALALD L DLALALALD L DLALD L DLALD L DLALALALD
L DLALD
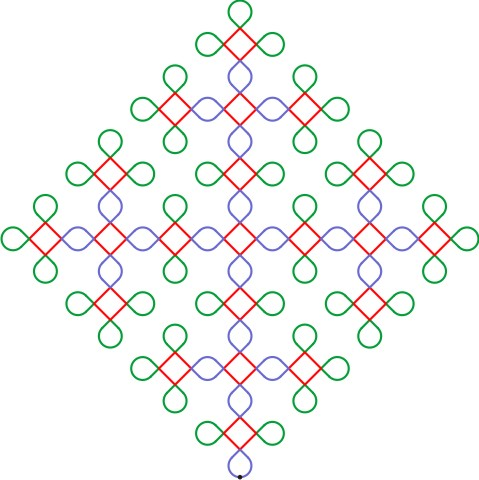
Traduzindo para a linguagem gráfica, obtemos a figura:
Etapa k = 3:
Substituímos as regras de reescrita na curva de iteração k = 2, encontraremos uma sequência de 681 operações.
Observando as etapas acima, podemos observar um padrão em relação à quantidade de operações. Para a etapa k = 0 temos 9 operações, que equivale à curva original; para a etapa k = 1, temos 41 operações; para a etapa k = 2, temos 169 operações; para a etapa k = 3, temos 681 operações. Podemos montar uma tabela comparativa:
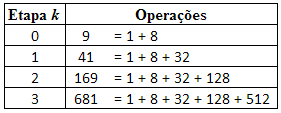 A partir desses dados experimentais, podemos concluir que para a etapa k = n, vale o somatório:
A partir desses dados experimentais, podemos concluir que para a etapa k = n, vale o somatório:
Podemos provar este resultado por indução finita. Vejamos uma forma fechada para a expressão acima. Seja:
Então:
Fazemos agora uma substituição de variáveis. Seja i = j +1:
De modo que:
Segue de (1) e (2) que:
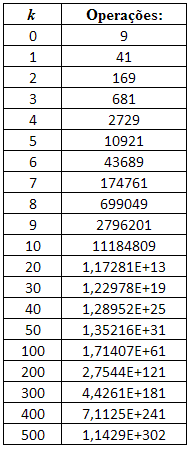
A partir da fórmula dada em (3), podemos construir uma tabela de k iterações:
Vemos que o crescimento de operações é exponencial e cresce muito rápido. Na décima iteração temos um pouco mais de 11 milhões de operações!
Encontrei na internet um blog bem bacana dedicado inteiramente às figuras Kolam.
Como foi observado pelo Aloísio Teixeira, a série dos kn termos da operações, é uma sequência mista de razão geométrica q = 4 e razão aritmética r = 5. Para saber mais, veja o artigo Progressão Mista no blog Elementos de Teixeira.
Referências:
[1] Scientifc American – Edição Especial Nº 11 – Etnomatemática
Veja mais:
A Fórmula de Pick e a Aproximação de π
Método da Multiplicação dos Camponeses Russos
A Astronomia e os Astrônomos da Grécia Antiga





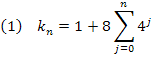
![clip_image002[4] clip_image002[4]](http://lh5.ggpht.com/-EaOWnRUse4A/UIPiKuoXDJI/AAAAAAAAWkc/NXXwNUOcj6Q/clip_image0024_thumb%25255B2%25255D.gif?imgmax=800)
![clip_image002[6] clip_image002[6]](http://lh6.ggpht.com/-bcjJPla6_Lk/UIPiM0t7HgI/AAAAAAAAWkk/XXuDsLDkrh4/clip_image0026_thumb%25255B4%25255D.gif?imgmax=800)
![clip_image002[8] clip_image002[8]](http://lh5.ggpht.com/-9qaCqi5fOG0/UIPiOy9-XpI/AAAAAAAAWks/2czzJacl5FA/clip_image0028_thumb%25255B2%25255D.gif?imgmax=800)
![clip_image002[10] clip_image002[10]](http://lh5.ggpht.com/-13JHPNh_NsU/UIPiQkQv5nI/AAAAAAAAWk0/94xyHzRKXD0/clip_image00210_thumb%25255B2%25255D.gif?imgmax=800)

Olá, Kleber!!!!
ResponderExcluirÓtima postagem, meu amigo e parceiro!!!!! Vejam só!!!! Uns diagramas tão antigos, traços contínuos simples (????) e... de certo modo, tal como os "quadrados mágicos" (matrizes quadradas, planilha), no entanto, chegam a se tornarem... indispensáveis, para tocar o progresso da humanidade!!!!
Depois, que você me repassou essa publicação através de e-mail, fiquei procurando-a e finalmente, consegui adquirir um exemplar impresso!!!! É muito boa e me será importante para as minhas "pesquisas" e futuras postagens para o meu blog!!!!
Gostou do "manjar dos deuses" que publiquei???? Estou ansioso para saber a sua opinião e de outros amigos, sobre a solução aritmética ( muitos de vocês esperaram 20 anos) para o desafio matemático impossível... o "Big Susto"!!!!!
Um abraço!!!!
Olá Valdir!
ResponderExcluirMuito interessante os Kolam, não? Há tempos queria fazer uma publicação. Acho que faltava inspiração. Tem muito mais informação a ser estudada. Com tempinho vou ver se faço mais um post.
Que bom que conseguiu a revista. Sabia que iria gostar.
Preciso ler com mais calma seu artigo, quero entender o que você fez lá.
Obrigado pelo prestígio. Um grande abraço!
Oi, Kleber!
ResponderExcluirAntes de mais nada, parabéns pelo artigo! Foi muito bem elaborado com riquezas de detalhes. Através dele conheci um pouco da cultura indiana. Os braceletes de Krishna são fascinates e o que me chamou mais atenção foi a matemática envolvida.
Esta fórmula do número de operações [;K_n;] em função do número [;k;] de etapas, ou seja, [;k=\frac{32}{3}.4^n-\frac{5}{3};] me fez lembrar um post meu sobre sequências mistas: http://elementosdeteixeira.blogspot.com.br/2012/09/070-progressao-mista_12.html.
Percebi então que a sequência (9,41,169,...) é uma sequência mista de razão geométrica [;q=4;] e razão aritmética [;r=5;]. Exemplo [;41=9.4+5;].
Um abraço!
Olá Aloísio, que bom que gostou e ainda melhor ter notado a correlação com uma progressão mista. Conforme o bem elaborado artigo de seu blog, temos:
ResponderExcluirSeja $a_1=9$, $q=4$ e $r=5$, onde $a_1$ é o primeiro termo da sequência, $q$ é a razão geométrica e $r$ é a razão aritmética. Assim:
$a_1=9$
$a_2=a_1 \cdot q + r=9 \cdot 4+5=41$
$a_3=a_2 \cdot q + r=41 \cdot 4+5=681$
$a_4=a_3 \cdot r + r=681 \cdot 4 +5 = 2729$
$a_n=a_{n-1} \cdot 4 + 5$
Não é à toa que matemáticos se interessem por estes tipos de figuras. Riqu[issimas em análise matemática.
Obrigado e um grande abraço!
Lembra muito linguagens formais e autômatos o procedimento de construção das figuras. O alfabeto aceito pelo autômato construtor é (L,D,A). Post muito interessante, parabéns!
ResponderExcluirObrigado Rycnda pelo prestígio. Esta é só uma pequena parte do artigo publicado na Scientific American. Dei uma focada nos braceletes de Krishna e um tratamento matemática nas iterações. Pretendo em breve escrever sobre as "serpentes".
ResponderExcluirUm abraço!