Por: Sebastião Vieira do Nascimento (Sebá)
Este artigo foi enviado pelo professor Sebá envolvendo a resolução de equações dos tipos:
Por ser um estudo extenso, resolvi dividi-lo em três partes para que fique mais fácil a leitura.
As equações acima foram criadas e batizadas como Equações de Sebá, que elaborou dois teoremas e os batizou-os como Teoremas de Sebá. A seguir, veremos primeiro a demonstração para o primeiro dos dois teoremas. No segundo artigo da série, veremos o segundo teorema e na terceira parte, veremos a Equação de Sebá estendida e algumas aplicações no mercado financeiro.
Teorema de Sebá 1: A equação An + Bn = Cm admite soluções naturais para m e n primos entre si.
Demonstração:
Seja a equação:
sendo a, b, c, n e m inteiros positivos. Multiplicando ambos os membros da equação (1) por:
obtém-se:
Substituindo o valor de da (1) em (2), obtém-se:
ou
Se escolhermos valores para a e b tal que a ≤ b ou a ≥ b, e substituirmos na (3), obtém-se valores inteiros positivos para A, B e C.
Método de Resolução da Equação de Sebá do Tipo An + Bn = Cm
Exemplo 1: Seja dividir um quadrado em dois cubos de várias maneiras diferentes. Seja a equação:
Considere a equação:
Multiplicando ambos os membros da equação acima por:
temos:
Comparando a equação (5) com a equação (4), devemos decompor m em potências de 3 e m + 1 em potências de 2. Isso só será possível se m e m + 1 forem, respectivamente, múltiplos de 3 e 2. Logo:
Assim, a equação (5) fica:
Logo, as soluções da equação dada são obtidas fazendo:
Por exemplo, se a = 1 e b = 3, temos que:
Verificação:
Vejamos algumas ternas geradas a partir da Equação de Sebá:
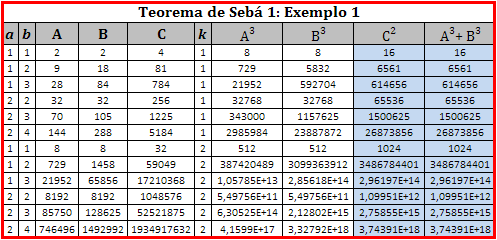 Observem que, se k = 1, os valores de C2 aumentam muito quando variamos os valores de a e b; e que aumentam vertiginosamente quando k = 2.
Observem que, se k = 1, os valores de C2 aumentam muito quando variamos os valores de a e b; e que aumentam vertiginosamente quando k = 2.
Exemplo 2: Seja dividir uma biquadrada em maneiras diferentes.
De forma análoga ao exemplo anterior, para a equação:
Consideremos a equação:
Multiplicando ambos os membros da equação acima por:
temos:
Comparando a equação (7) com a equação (6), devemos decompor m em potências de 3 e m + 1 em potências de 4. Isso só é possível se m e m + 1, respectivamente, forem múltiplos de 3 e 4. Logo:
Assim, a equação (7) fica:
Logo, as soluções da equação dada são obtidas fazendo:
Verificação:
Vejamos algumas ternas geradas a partir da Equação de Sebá:
Assim como ocorre para uma equação quadrada como soma de dois cubos, esta, uma biquadrada como soma de dois cubos, os valores crescem rapidamente.
Nos próximo artigo veremos a resolução das equações de Sebá do tipo:
Este artigo foi cedido gentilmente por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB, além de colaborador deste blog. Foram feitas algumas alterações do manuscrito original para melhor exposição.
Veja mais:
Método de Sebá para Resolução de Alguns Casos Particulares de Equações Diofantinas Lineares
Critérios de Divisibilidade por Qualquer Número Primo Maior que 11
O Problema da Doação dos Terrenos e os Ternos Pitagóricos
Deserto Entre Números Primos

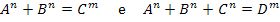


Oi, Kleber!
ResponderExcluirInteressante a resolução desta equação diofantina. São estes tipos de elocubrações que Fermat se empenhava na época.
As equações de Sebá são importantes também na medida em que se compreende a grande dificuldade que é de se demonstrar o UTF, tendo em vista que, se n=m, os números não são primos entre si.
Oi, Kleber!
ResponderExcluirExclui o comentário anterior porque errei no LATEX.
Olha só o que o Paulinho da Matemática ( que conheci no face ) me mostrou.
Desde que o [;UTF;] foi efetivamente demonstrado por Willes, ele pode ser usado para demonstrar muita coisa, por exemplo,
a irracionalidade da raíz enésima de [;2;]. Veja:
RAÍZ ENÉSIMA DE [;2=\frac{a}{b};], com [;a;] e [;b;] inteiros positivos.
Elevando ambos os membros à [;n;], temos
[;2=\frac{a^n}{b^n}\Rightarrow 2b^n=a^n \Rightarrow b^n+b^n=a^n;], o que não é possível pelo [;UTF;]
Legal, né.
Valeu.
Realmente muito legal e muito simples! O Matemático é um ser muito interessante mesmo, consegue fazer coisas incríveis com os números! Então, tudo que conseguirmos reduzir a uma igualdade do tipo $A^n+B^n=C^n$ $\forall n> 2$, podemos concluir sua impossibilidade. Incrível a simplicidade. Acho que este tipo de pensamento combina muito com as coisas que você anda fazendo em seu blog, não?
ResponderExcluirObrigado por compartilhar. Abraços!