Ficou provado que é impossível a construção de um quadrado com mesma área que um círculo utilizando instrumentos euclidianos. O que conseguimos são somente boas aproximações. Encontrar um segmento de reta que aproxime $\pi$ também mobiliza muitos matemáticos.
Este método que apresento aqui foi desenvolvido por mim e aproxima $\pi$ em duas casas decimais, levando ao valor de $3,14093$. Vamos ver como se constrói este segmento.
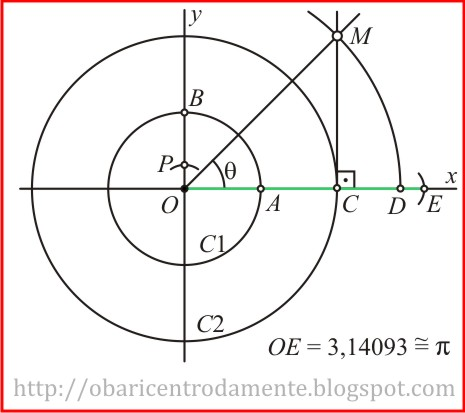
Construção
$1)$ Inicie a construção num eixo ortogonal $xOy$;
$2)$ Descreva a circunferência $C_1$ de centro $O$ e raio $1$ e marque os ponto $A$ e $B$ na intersecção com as retas $Ox$ e $Oy$, respectivamente;
$3)$ Descreva a circunferência $C_2$ de centro $O$ e raio $2OA = 2$ e marque o ponto $C$ na intersecção com a reta $Ox$;
$4)$ Trace a bissetriz do ângulo $AOB$. Assim o ângulo $\theta=45°$;
$5)$ Suba a perpendicular ao eixo $x$ por $C$ e marque o ponto $M$ na intersecção com a bissetriz;
$6)$ Descreva um arco de raio $OM$ centrado em $O$ e marque o ponto $D$ na intersecção com a reta $Ox$;
$7)$ Construindo sucessivas mediatrizes convenientes, encontramos o ponto $P$ em $Oy$ de modo que $OP$ seja $5/16$ do raio de $C_1$;
$8)$ Com raio $OP$ e centro em $D$, descreva um arco marcando o ponto $E$ na intersecção com $Ox$.
$9)$ O Segmento $OE$ aproxima $\pi$ em $3,14093$.
Demonstração
Como o ângulo $\theta=45°$ e $CM$ é ortogonal ao eixo $x$, temos que $OC = CM = 2$. Assim:
\begin{matrix}
OM^2=OC^2+CM^2\\
OM^2=4+4\\
OM=2\sqrt{2}
\end{matrix}
Vejam que $OM = OD$. O segmento $OE = OD + DE$. O segmento $OD$ já encontramos e o segmento $DE = OP = 5/16$. Assim:
\begin{matrix}
OE=OD+DE\\
OE=2\sqrt{2}+\frac{5}{16}\\
OE=3,14093 \cong \pi
\end{matrix}
Veja mais:
Retificação da Circunferência (Parte 1)
Retificação da Circunferência (Parte 2) - Método de Kochanski
Retificação da Circunferência (Parte 3) - Método de Gelder



Muito engenhoso, Kleber! Muito bom vc ter compartilhado esta pérola!!
ResponderExcluirAcho importante divulgar pequenas ideias. Às vezes alguém poderá se benificiar.
ResponderExcluirUm abraço.
Oi Kleber! Como matemático sofre! Tem que tentar resolver, achar que não dá, provar que não dá e ainda achar um método alternativo. Por falar em sofrer certa vez meu professor de geometria do cursinho confessou-se incapaz de resolver um problema e me passou, era um problema de aparência simples: construir com régua e compasso uma tangente a uma circunferência sob certa condição... Rapaz! o diabo do problema era refratário a tudo que eu conhecia e pior, o problema grudou em mim e eu nele... entrei na faculdade, cursei um ano, tranquei, casei, perguntei, consultei, voltei e...NADA. Quatro anos depois eu estava debruçado sobre o problema e notei: Um ângulo que se formaria se eu resolvesse o problema media 1/3 de um ângulo que estava lá desde o começo então EUREKA! Se eu resolvesse o problema com régua e compasso teria inventado um método para trissecar um ângulo, como isso não é possível, então a construção pretendida também não...Isso é que é sofrer...mas a gente gosta né!
ResponderExcluirE como gostamos! O que seria de um matemáticos sem os problemas? Eu, assim como inúmeros outros, já gastei muitas horas a fim de "inventar" um método para trissecção. Claro que desisti. Mas particularmente, este problema da retificação da circunferência eu acho muito interessante e ainda me pego tentando aproximações. Consegui no máximo 2 casas e esta resolução é uma delas. Mas continuo tentando. Quero uma retificação aproximada, levando $\pi$ a 8 casas decimais. Quem sabe algum dia consigo.
ResponderExcluirCaso ainda se lembre, poderia postar aqui para todos nós este seu problema. Afinal, somos curiosos e gostamos muito disso!
Abraços.
Oi Kleber! Com a idade que estou é difícil pensar sobre um problema mais de 2 horas sem ter uma grande dor de cabeça física mesmo! Os problemas e as invenções da minha vida estão num caderninho. Sou uma nulidade em informática, para se ter uma ideia nunca mandei um e-mail. Vou tentar descrever o problema: Do lado esquerdo de uma folha desenhe uma circunferência, trace uma secante vertical a ela, do lado direito da secante coloque um ponto P. O problema não especificava as distâncias. Pedia-se: Construir uma tangente à circunferência (do lado de cima) de modo que essa tangente encontre a secante em A e faça um ângulo reto com o segmento AP. Quanto à quadratura certa vez pensei num processo iterativo que retificasse um quadrado inscrito e outro circunscrito, depois um octógono inscrito e outro circunscrito, depois um 16-gono etc assim eu teria um intervalo para pi, mas ficou só na intenção. Se for de interesse vou ver se falo com alguém para mandar a solução do problema. Abraço
ExcluirNão precise se preocupar. O método de inserir um círculo entre 2 n-ágonos que você mencionou é conhecida. Arquimedes usou muito este método. Tinha me interessado inicialmente no problema da tangente. Vou tentar esboçar alguma coisa encima dos seus dados.
ResponderExcluirObrigado novamente pela resposta!
Abraços.
Kleber! Esqueci de te passar alguns detalhes do problema da tangente:O centro da circunferência "O" está em semiplano oposto a P em relação à secante, para visualizar melhor o ângulo triplo faça o seguinte: Seja B a intersecção mais abaixo da circunferência com a secante, trace a reta OB, coloque P nesta reta de modo que OB=BP. Não há quebra lógica nisso visto que o problema era para um lugar qualquer de P então, em particular, seria resolvido para essa nova posição de P
ResponderExcluir