Um número de Smith é um número composto cuja soma S(N) dos algarismos deste número é igual à soma Sp(N) dos algarismos de seus fatores primos.
Por exemplo: dado o número N = 27, vamos verificar se este é um número de Smith.
Somamos os algarismos de 27:
O número 27 pode ser escrito na forma de produto entre seus fatores primos:
A soma de seus fatores primos será:
Verificamos que 27 é um número de Smith:
Albert Wilansky, da Universidade de Lehigh, observou esta propriedade no número de telefone de seu irmão Harold Smith. O número é 4937775:
O número 4937775 pode ser escrito na forma de produto entre seus fatores primos:
Portanto:
Wilansky constatou que existem 360 números de Smith menores que 10.000. No entanto, ele se enganou, pois na verdade, há 376 números de Smith menores que 10.000:
4, 22, 27, 58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 378, 382, 391, 438, 454, 483, 517, 526, 535, 562, 576, 588, 627, 634, 636, 645, 648, 654, 663, 666, 690, 706, 728, 729, 762, 778, 825, 852, 861, 895, 913, 915, 922, 958, 985, 1086, 1111, 1165, 1219, 1255, 1282, 1284, 1376, 1449, 1507, 1581, 1626, 1633, 1642, 1678, 1736, 1755, 1776, 1795, 1822, 1842, 1858, 1872, 1881, 1894, 1903, 1908, 1921, 1935, 1952, 1962, 1966, 2038, 2067, 2079, 2155, 2173, 2182, 2218, 2227, 2265, 2286, 2326, 2362, 2366, 2373, 2409, 2434, 2461, 2475, 2484, 2515, 2556, 2576, 2578, 2583, 2605, 2614, 2679, 2688, 2722, 2745, 2751, 2785, 2839, 2888, 2902, 2911, 2934, 2944, 2958, 2964, 2965, 2970, 2974, 3046, 3091, 3138, 3168, 3174, 3226, 3246, 3258, 3294, 3345, 3366, 3390, 3442, 3505, 3564, 3595, 3615, 3622, 3649, 3663, 3690, 3694, 3802, 3852, 3864, 3865, 3930, 3946, 3973, 4054, 4126, 4162, 4173, 4185, 4189, 4191, 4198, 4209, 4279, 4306, 4369, 4414, 4428, 4464, 4472, 4557, 4592, 4594, 4702, 4743, 4765, 4788, 4794, 4832, 4855, 4880, 4918, 4954, 4959, 4960, 4974, 4981, 5062, 5071, 5088, 5098, 5172, 5242, 5248, 5253, 5269, 5298, 5305, 5386, 5388, 5397, 5422, 5458, 5485, 5526, 5539, 5602, 5638, 5642, 5674, 5772, 5818, 5854, 5874, 5915, 5926, 5935, 5936, 5946, 5998, 6036, 6054, 6084, 6096, 6115, 6171, 6178, 6187, 6188, 6252, 6259, 6295, 6315, 6344, 6385, 6439, 6457, 6502, 6531, 6567, 6583, 6585, 6603, 6684, 6693, 6702, 6718, 6760, 6816, 6835, 6855, 6880, 6934, 6981, 7026, 7051, 7062, 7068, 7078, 7089, 7119, 7136, 7186, 7195, 7227, 7249, 7287, 7339, 7402, 7438, 7447, 7465, 7503, 7627, 7674, 7683, 7695, 7712, 7726, 7762, 7764, 7782, 7784, 7809, 7824, 7834, 7915, 7952, 7978, 8005, 8014, 8023, 8073, 8077, 8095, 8149, 8154, 8158, 8185, 8196, 8253, 8257, 8277, 8307, 8347, 8372, 8412, 8421, 8466, 8518, 8545, 8568, 8628, 8653, 8680, 8736, 8754, 8766, 8790, 8792, 8851, 8864, 8874, 8883, 8901, 8914, 9015, 9031, 9036, 9094, 9166, 9184, 9193, 9229, 9274, 9276, 9285, 9294, 9296, 9301, 9330, 9346, 9355, 9382, 9386, 9387, 9396, 9414, 9427, 9483, 9522, 9535, 9571, 9598, 9633, 9634, 9639, 9648, 9657, 9684, 9708, 9717, 9735, 9742, 9760, 9778, 9840, 9843, 9849, 9861, 9880, 9895, 9924, 9942, 9968, 9975, 9985.
Uma observação é que o suposto número da Besta 666 também é um número de Smith.
Os números de Smith podem ser classificados em vários tipos:
Número de Smith Semiprimo
Um número semiprimo ou biprimo é aquele que é composto pelo produto de dois números primos. Um número de Smith semiprimo são aqueles que obedecem à propriedade de um número de Smith e que são produtos entre dois números primos.
Por exemplo:
Todos os números de Smith semiprimos menores que 104 são:
4, 22, 58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 382, 391, 454, 517, 526, 535, 562, 634, 706, 778, 895, 913, 922, 958, 985, 1111, 1165, 1219, 1255, 1282, 1507, 1633, 1642, 1678, 1795, 1822, 1858, 1894, 1903, 1921, 1966, 2038, 2155, 2173, 2182, 2218, 2227, 2326, 2362, 2434, 2461, 2515, 2578, 2605, 2614, 2722, 2785, 2839, 2902, 2911, 2965, 2974, 3046, 3091, 3226, 3442, 3505, 3595, 3622, 3649, 3694, 3802, 3865, 3946, 3973, 4054, 4126, 4162, 4189, 4198, 4279, 4306, 4369, 4414, 4594, 4702, 4765, 4855, 4918, 4954, 4981, 5062, 5071, 5098, 5242, 5269, 5305, 5386, 5422, 5458, 5485, 5539, 5602, 5638, 5674, 5818, 5854, 5926, 5935, 5998, 6115, 6178, 6187, 6259, 6295, 6385, 6439, 6457, 6502, 6583, 6718, 6835, 6934, 7051, 7078, 7186, 7195, 7249, 7339, 7402, 7438, 7447, 7465, 7627, 7726, 7762, 7834, 7915, 7978, 8005, 8014, 8023, 8077, 8095, 8149, 8158, 8185, 8257, 8347, 8518, 8545, 8653, 8851, 8914, 9031, 9094, 9166, 9193, 9229, 9274, 9301, 9346, 9355, 9382, 9427, 9535, 9571, 9598, 9634, 9742, 9778, 9895, 9985, ...
Número de Smith Palíndromo
Uma frase palíndroma, ou capicual, é aquela que lida da direita para esquerda ou vice-versa tem o mesmo sentido.
Os números, assim como letras, podem ser classificados como palíndromos. Dentre os números de Smith também são encontrados números de palíndromos. Por exemplo: 4, 22, 121, 202.
Todos os números de Smith Palíndromos menores que 106 são:
4, 22, 121, 202, 454, 535, 636, 666, 1111, 1881, 3663, 7227, 7447, 9229, 10201, 17271, 22522, 24142, 28182, 33633, 38283, 45054, 45454, 46664, 47074, 50305, 51115, 51315, 54645, 55055, 55955, 72627, 81418, 82628, 83038, 83938, 90409, 95359, 96169, 164461, 173371, 239932, 256652, 262262, 294492, 362263, 373373, 445544, 454454, 505505, 515515, 535535, 545545, 635536, 704407, 717717, 832238, 841148, 864468, 951159, 956659, 974479 e 983389.
Números de Smith Reversíveis
Um número reverso é aquele obtido pela inversão de seus algarismos. Por exemplo: 123 e 321 são números reversos.
Um número de Smith reversível é aquele cujo reverso também é um número de Smith. Por exemplo: 58 e 85.
Todos os números de Smith reversíveis menores que 104 são:
4, 22, 58, 85, 121, 202, 265, 319, 454, 535, 562, 636, 666, 913, 1111, 1507, 1642, 1881, 1894, 1903, 2461, 2583, 2605, 2614, 2839, 3091, 3663, 3852, 4162, 4198, 4369, 4594, 4765, 4788, 4794, 4954, 4974, 4981, 5062, 5386, 5458, 5539, 5674, 5818, 5926, 6295, 6439, 6835, 7051, 7227, 7249, 7438, 7447, 8158, 8185, 8347, 8518, 8545, 8874, 8914, 9229, 9346, 9355, 9382, 9427 e 9634.
Podemos perceber que os números palíndromos de Smith são casos particulares dos números de Smith reversíveis.
Números de Smith – Fibonacci
Os números de Fibonacci que também são números de Smith podem ser chamados de Números de Smith – Fibonacci. Durante os cálculos, foi observado que o menor número de Smith – Fibonacci é 1346369:
Temos que:
e
Logo:
Ainda há outros números de Smith – Fibonacci:
Números de Smith Abundantes
Um número abundante todo número natural n cuja soma dos seus divisores próprios é superior a n. O primeiro número abundante é o 12, porque sendo os seus divisores próprios 1, 2, 3, 4 e 6, a soma destes é 1 + 2 + 3 + 4 + 6 = 16 > 12.
Se um número de Smith tem esta característica é chamado de número de Smith Abundante. Por exemplo, o número 438 é um número abundante, pois:
Como vimos, a soma dos divisores de 438 é maior que ele próprio.
Todos os números de Smith abundantes menores que 104 são:
378, 438, 576, 588, 636, 648, 654, 666, 690, 728, 762, 852, 1086, 1284, 1376, 1626, 1736, 1776, 1842, 1872, 1908, 1952, 1962, 2286, 2484, 2556, 2576, 2688, 2934, 2944, 2958, 2964, 2970, 3138, 3168, 3174, 3246, 3258, 3294, 3366, 3390, 3564, 3690, 3852, 3864, 3930, 4428, 4464, 4472, 4592, 4788, 4794, 4880, 4960, 4974, 5088, 5172, 5248, 5298, 5388, 5526, 5772, 5874, 5936, 5946, 6036, 6054, 6084, 6096, 6188, 6252, 6344, 6684, 6702, 6760, 6816, 6880, 7026, 7062, 7068, 7674, 7764, 7782, 7784, 7824, 7952, 8154, 8196, 8372, 8412, 8466, 8568, 8628, 8680, 8736, 8754, 8766, 8790, 8792, 8874, 9036, 9184, 9276, 9294, 9296, 9330, 9396, 9414, 9522, 9648, 9684, 9708, 9760, 9840, 9880, 9924, 9942 e 9968.
Números de Smith Deficientes
Um número deficiente é todo número natural n cuja soma dos seus divisores próprios é inferior a n. O número 10 é um número deficiente, porque sendo os seus divisores próprios 1, 2, e 5, a soma destes é 1 + 2 + 5 = 8 < 10.
Se um número de Smith tem esta característica é chamado de número de Smith Deficiente. Por exemplo, o número 22 é um número deficiente, pois:
Como vimos, a soma dos divisores de 22 é menor que ele próprio.
Todos os números de Smith deficientes menores que 104 são:
4, 22, 27, 58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 382, 391, 454, 483, 517, 526, 535, 562, 627, 634, 645, 663, 706, 729, 778, 825, 861, 895, 913, 915, 922, 958, 985, 1111, 1165, 1219, 1255, 1282, 1449, 1507, 1581, 1633, 1642, 1678, 1755, 1795, 1822, 1858, 1881, 1894, 1903, 1921, 1935, 1966, 2038, 2067, 2079, 2155, 2173, 2182, 2218, 2227, 2265, 2326, 2362, 2366, 2373, 2409, 2434, 2461, 2475, 2515, 2578, 2583, 2605, 2614, 2679, 2722, 2745, 2751, 2785, 2839, 2888, 2902, 2911, 2965, 2974, 3046, 3091, 3226, 3345, 3442, 3505, 3595, 3615, 3622, 3649, 3663, 3694, 3802, 3865, 3946, 3973, 4054, 4126, 4162, 4173, 4185, 4189, 4191, 4198, 4209, 4279, 4306, 4369, 4414, 4557, 4594, 4702, 4743, 4765, 4832, 4855, 4918, 4954, 4959, 4981, 5062, 5071, 5098, 5242, 5253, 5269, 5305, 5386, 5397, 5422, 5458, 5485, 5539, 5602, 5638, 5642, 5674, 5818, 5854, 5915, 5926, 5935, 5998, 6115, 6171, 6178, 6187, 6259, 6295, 6315, 6385, 6439, 6457, 6502, 6531, 6567, 6583, 6585, 6603, 6693, 6718, 6835, 6855, 6934, 6981, 7051, 7078, 7089, 7119, 7136, 7186, 7195, 7227, 7249, 7287, 7339, 7402, 7438, 7447, 7465, 7503, 7627, 7683, 7695, 7712, 7726, 7762, 7809, 7834, 7915, 7978, 8005, 8014, 8023, 8073, 8077, 8095, 8149, 8158, 8185, 8253, 8257, 8277, 8307, 8347, 8421, 8518, 8545, 8653, 8851, 8864, 8883, 8901, 8914, 9015, 9.031, 9.094, 9.166, 9.193, 9.229, 9.274, 9.285, 9.301, 9.346, 9.355, 9.382, 9.386, 9.387, 9.427, 9.483, 9.535, 9.571, 9.598, 9.633, 9.634, 9.639, 9.657, 9.717, 9.735, 9742, 9778, 9843, 9849, 9861, 9895, 9975 e 9985.
Números de Smith Quadrados
Um número de Smith que é um quadrado perfeitos pode ser denominado como número de Smith quadrado.
Todos os números de Smith quadrados menores que 107 são:
4, 121, 576, 729, 6084, 10201, 17424, 18496, 36481, 51529, 100489, 124609, 184041, 195364, 410881, 559504, 674041, 695556, 732736, 887364, 896809, 966289, 988036, 1038361, 1190281, 1238769, 1726596, 1852321, 2166784, 2975625, 3407716, 3613801, 3663396, 3849444, 3888784, 3892729, 4088484, 4309776, 4330561, 4809249, 4875264, 4888521, 5031049, 5225796, 5391684, 5438224, 5461569, 5527201, 5978025, 6517809, 6630625, 6635776, 6780816, 6864400, 6969600, 7059649, 7273809, 7717284, 7868025, 7946761, 8048569, 8567329, 8573184, 8608356, 9150625, 9455625, 9678321 e 9960336.
Números de Smith Cúbicos
Um número de Smith que é um cubo perfeito pode ser denominado como número d Smith cúbico.
Todos os números de Smith cúbicos menores que 1010 são:
27, 729, 19683, 474552, 7077888, 7414875, 8489664, 62099136, 112678587, 236029032, 246491883, 257259456, 279726264, 345948408, 463684824, 567663552, 638277381, 721734273, 766060875, 988047936, 1177583616, 1412467848, 2131746903, 2493326016, 2714704875, 3023464536, 3215578176, 3294646272, 3951805941, 4443297984, 4843965888, 4895680392, 6158676537, 8266914648, 8340725952, 8792838144 e 8831234763.
Números de Smith Triangulares
Um número triangular é um número natural que pode ser representado na forma de triângulo. Foi desenvolvido por Gauss em 1788 quando tinha apenas 10 anos.
*
* *
* * *
Os primeiros números triangulares são: 1, 3, 6, 10, 15, 21, ...
O n-ésimo número triangular é dado por:
Os números de Smith também apresentam características triangulares e são denominados números de Smith triangulares.
Todos os números de Smith triangulares menores que 107 são:
378, 666, 861, 2556, 5253, 7503, 10296, 16653, 27261, 28920, 29890, 32896, 46056, 72771, 84255, 85905, 92235, 94395, 120786, 132870, 141778, 157641, 215496, 328455, 345696, 385881, 386760, 396495, 424581, 529935, 533028, 588070, 654940, 682696, 683865, 723003, 778128, 866586, 885115, 897130, 941878, 959805, 977901, 993345, 1082656, 1134771, 1234806, 1398628, 1457778, 1466328, 1495585, 1528626, 1570878, 1597578, 1633528, 1680861, 1792671, 1875016, 1876953, 1925703, 1931595, 1983036, 2087946, 2089990, 2137278, 2273778, 2351196, 2396955, 2458653, 2692360, 2828631, 2859636, 2890810, 2924571, 2968266, 3296028, 3378700, 3383901, 3451878, 3467661, 3579150, 3654456, 3733278, 3757911, 3904615, 3935415, 4119885, 4444671, 4710915, 4887501, 4925091, 5492955, 5586153, 5592840, 5815755, 6725278, 6984453, 7051890, 7486515, 7505875, 7536903, 7583565, 7850703, 7858630, 8090253, 8158780, 8211378, 8280415, 8284485, 8341570, 8390656, 8398851, 8485140, 8501626, 8982441, 9281586, 9359301, 9541896, 9651421 e 9677800.
Números de Smith Repdigit
Todos os números de Smith que possuem todos os algarismos iguais são denominados como números de Smith Repdigit. Todos os números de Smith repdigit menores que 1060 são:
4, 22, 666, 1111, 6666666, 4444444444, 44444444444444444444, 555555555555555555555555555, 55555555555555555555555555555555 e 4444444444444444444444444444444444444444444444444444444.
Números de Smith Consecutivos
Os números de Smith que são consecutivos também podem ser denominados como números de Smith consecutivos. Por exemplo: o par de números 728 e 729.
Todos os números de Smith consecutivos menores que 105 são:
(728, 729), (2964, 2965), (3864, 3865), (4959, 4960), (5935, 5936), (6187, 6188), (9386, 9387), (9633, 9634), (11.695 , 11696), (13764, 13765), (16536, 16537), (16591, 16592), (20784, 20785), (25428, 25429), (28808, 28809), (29623, 29624), (32696, 32697 ), (33632, 33633), (35805, 35806), (39585, 39586), (43736, 43737), (44733, 44734), (49027, 49028), (55344, 55345), (56336, 56337), (57663, 57664), (58305, 58306), (62634, 62635), (65912, 65913), (65974, 65975), (66650, 66651), (67067, 67068), (67728, 67729), (69.279 , 69280), (69835, 69836), (73615, 73616), (73616, 73617), (74168, 74169), (74298, 74299), (76495, 76496), (76911, 76912), (77385, 77386 ), (78744, 78745), (82488, 82489), (82640, 82641), (83744, 83745), (83928, 83929), (83937, 83938), (84759, 84760), (84882, 84883), (85135, 85136), (87362, 87363), (87855, 87856), (89743, 89744), (89904, 89905), (90228, 90229), (90872, 90873), (91255, 91256), (91.364 , 91365), (91488, 91489), (93275, 93276), (93471, 93472), (94094, 94095), (94184, 94185), (94584, 94585), (95277, 95278), (95984, 95985 ), (96151, 96152), (96921, 96922), (97915, 97916), (98022, 98023) e (98.900, 98.901).
Existem 615.885 números de Smith consecutivos menores que 109.
Números de Smith Triplos
Quando há três números de Smith que são consecutivos também podem ser denominados como números de Smith triplos. Por exemplo: o terno de números (73.615; 73.616; 73.617). Todos os números de Smith triplos menores que 106 são:
(73615, 73616, 73617), (209065, 209066, 209067), (225951, 225952, 225953), (283745, 283746, 283747), (305455, 305456, 305457), (342879, 342880, 342881), (656743, 656744, 656745), (683670, 683671, 683672), (729066, 729067, 729068), (747948, 747949, 747950), (774858, 774859, 774860), (879221, 879222, 879223) e (954590, 954591, 954592).
Existem 15.955 números de Smith triplos menores que 109.
Números de Smith Quádruplos
Quando há quatro números de Smith que são consecutivos também podem ser denominados como números de Smith quádruplos. O menor conjunto de números de Smith quádruplos é:
(4463535, 4463536, 4463537, 4463538)
Abaixo estão somente os menores números dos conjuntos de números de Smith quádruplos menores que 108 são:
4463535, 6356910, 8188933, 9425550, 11148564, 15966114, 18542654, 21673542, 22821992, 23767287, 28605144, 36615667, 39227466, 47096634, 47395362, 48072396, 54054264, 55464835, 57484614, 57756450, 57761165, 58418508, 61843387, 62577157, 64572186, 65484066, 66878432, 67118680, 71845857, 75457380, 77247606, 78432168, 88099213, 89653781, 90166567 e 92656434.
Existem 384 números de Smith quádruplos menores que 109.
Números de Smith Quíntuplos
Quando há cinco números de Smith que são consecutivos também podem ser denominados como números de Smith quíntuplos. O menor conjunto de números de Smith quádruplos é:
(15966114, 15966115, 15966116, 15966117, 15966118)
Abaixo estão somente os menores números dos conjuntos de números de Smith quíntuplos menores que 109:
15966114, 75457380, 162449165, 296049306, 296861735, 334792990, 429619207, 581097690, 581519244, 582548088, 683474015, 809079150, 971285861 e 977218716.
Existem 14 números de Smith quíntuplos menores de 109.
Números de Smith Quíntuplos
Quando há cinco números de Smith que são consecutivos também podem ser denominados como números de Smith quíntuplos. O menor conjunto de números de Smith quádruplos é:
(15966114, 15966115, 15966116, 15966117, 15966118)
Números de Smith – k
Se existir k números de Smith consecutivos, estes podem ser denominados como números de Smith – k.
Você é capaz de encontrar o menor conjunto dos números de Smith – 6?
Veja mais:
5 Trilhões de Dígitos de PI
A Bolsa de Valores e a Sequência de Fibonacci
Construindo uma Sequência de Números Não-Primos



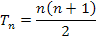

Muito interessante o post sobre os números de Smith. Eu não conhecia esses números, mas gosto muito dessas curiosidades. Parabéns!
ResponderExcluirObrigado Paulo. Achei na internet em páginas estrangeiras, mas como não havia encontrado no Brasil, resolvi compartilhar aqui no blog. Estou pesquisando outras curiosidades, logo publico aqui.
ResponderExcluirUm abraço!
Oi.Para que serve esses números de Smith?
ResponderExcluirAbraços,Lúcia
17/08/010
Olá Lúcia. Tecnicamente falando não passa de uma matemática recreativa, entrando aí numa categoria de curiosidades da Matemática. Mas o mais importante de tudo não é aonde ele é aplicado e sim como uma pessoa percebeu um padrão e encontrou uma algoritmo para encontrar mais número que obedeçam estes padrões. Essas coisas são assim mesmo: belas e intrigantes. Será que Fibonacci sabia que as abelhas se reproduzem seguindo a lei de sua sequência? Ou mesmo que um náultilo possui sua espiral? Crei que não. Hoje não sei se os número de Smith tem alguma utilidade prática para resolver problemas do cotidiano, mas talvez alguém algum dia veja essa aplicação.
ResponderExcluirAgradeço seu comentário e confiança neste blog.
Um abraço!
perfeito
ResponderExcluir